Hi Scott,

I think I understand.

Here is my diagram

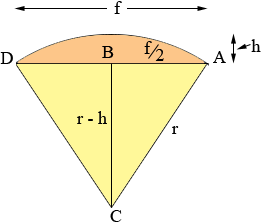
I am going to develop a general expression showing the quantities you sent in red.

In the diagram f is the width of the opening (f = 96 inches) and h is the rise of the arc (h = 18 inches). C is the centre of the circle that subtends the arc and r is the radius of the circle. Since triangle ABC is a right triangle Pythagoras Theorem gives (f/2)² + (r - h)² = r². Solving for the radius r gives

r = (f² + 4h²)/(8h) (r = 73 inches).

Again, since triangle ABC is a right triangle sin(angle BCA) = (f/2)/r so (angle BCA) = sin^-1(f/(2r) and

angle DCA = 2 sin^-1(f/(2r)) (angle DCA = 82.2^o)

Now suppose there are to be n window units (n = 5). Each window unit then subtends an angle of measure (angle DCA)/5. Call the measure of this angle t^o (t^o = 82.2/5 = 16.4^o). In the diagram below the line segment QP represents one window unit and S is the midpoint of QP. Let the width of the window be w units then |PS| = w/2.

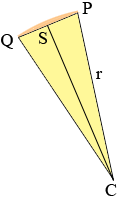
Since the measure of the angle QCP is t^o the measure of the angle SCP is t^o/2. Hence

|PS|/r = w/(2r) = sin(t^o/2) or

w = 2r sin(t^o/2) (w = 146 sin(16.4/2) = 20.9 inches).

I hope this helps,
Harley