Scott,

I am going to approach this using a tree diagram and only 3 rolls of the die so that my tree is not too large.

I see the tree as a process. You start at the bottom and roll the die. If you roll a 6 you climb the "6 branch" and if you don't roll a 6 you climb the "not 6" branch. The probability you climb the "6" branch is 1/6 and the probability you climb the "not 6" branch is 5/6.

Regardless of where you are you roll the die again and climb yo the "6" or "not 6" branches using the same rule. Finally roll the die a third time and climb to the third level using the same rule.

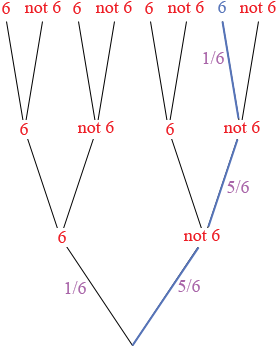
So here is your question. You are at the bottom of the tree and you are going to climb to the third level using the rules above. What is the probability that you take the blue path which is "not 6" followed by "not 6" followed by "6"? From the diagram it's (5/6) × (5/6) × (1/6). Can you express this probability as odds?

Harley