An isosceles triangle - Math Central

HOME

Math Central

Quandaries & Queries

Question from sela, a student:

An isosceles triangle has two equal sides of length 10 cm. Theta is the
angle between two equal sides.
a) Express area of a triangle as a function of theta
b) If theta is increasing at a rate of 10 degrees/minute, how fast is area
changing at the instant theta=pi/3?
c) at what value of theta will the triangle have the maximum area?

Sela,

I can get you started.

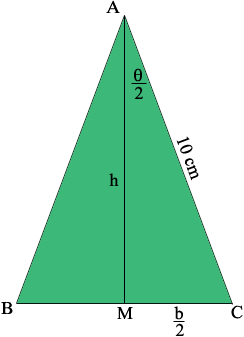
triangle

AM is perpendicular to BC and hence by the symmetry of this isosceles triangle |MC| = b/2 cm and the measure of angle CAM is θ/2 degrees. Thus cos(θ/2) = h/10 and sin(θ/2) = b/20. Hence the area of the triangle is

1/2 b × h = 100 sin(θ/2) cos(θ/2).

A trig identity will greatly simplify this expression. Do you know what it is?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.