| |||
| Math Central | Quandaries & Queries |
|
Question from stephanie, a student: Give parameterizations r(t)=x(t)i + y(t)j for the part of the parabola y=2x-x^2, from (2,0) to (0,0). Sketch the curve using arrows to show direction for increasing t. Ans: x=2-t, y=2(2-t)-(2-t)^2 |
Hi Stephanie,
You gave the answer as x = 2 - t, y = 2(2 - t) - (2 - t)2 but you missed an important part of the answer. You didn't give the domain of t and without it you don't know which part of the parabola you are parameterizing. You need to say
x = 2 - t, y = 2(2 - t) - (2 - t)2 for 0 ≤ t ≤ 2.
Now you can see that when t = 0, x = 2 and y = 0 and when t = 2, x = 0 and y = 0. Thus the parameterization is for the piece of the parabola from (2,0) to (0,0) but not only that, as t increases you are moving from (2,0) to (0,0).
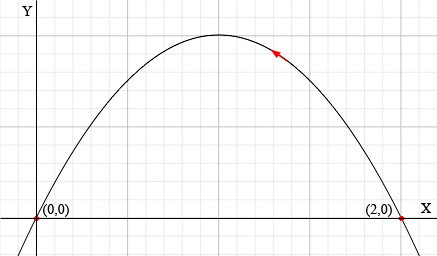
There are many ways to parameterize a curve and this is not the only answer to your problem. When I first read your problem I thought of the parameterization x = s and y = 2s - s2. In this case the point (2,0) comes from s = 2 and the point (0,0) comes from s = 0. Thus I get
x = s and y = 2s - s2 for 0 ≤ s ≤ 2.
With this parameterization as the parameter s increases you move along the curve from (0,0) to (2,0).
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.