Hi Stephanie,

This is a natural question for a student to ask and one for which I am not sure I have a very satisfactory answer. My answer as a mathematician is that (-2)(-4) = 8 is a consequence of the distributive law. The distributive law is so useful and it adds so much to the beauty and structure of arithmetic that I want it to be true in every case and hence (-2)(-4) = 8.

This is not a very satisfactory response and doesn't address your request for an example in "real life". (I really dislike this term! As a teacher you will most likely be doing mathematics every day of your life and I expect your life is as real as anyone else's. I have started using the term "math beyond school".) As I see it, the question amounts to "is there a use of arithmetic and an interpretation of multiplication where it is natural to multiply a negative number by a negative number?"

In many of the situations where we see negative numbers the concept of multiplication of two negatives is not natural. I think of temperature, my savings account where a deposit is positive and a withdrawal is negative, height above sea level and so on. I want to show you an interpretation of multiplication where the multiplication of two negative numbers is natural.

I am thinking of the number line and multiplication is an action, for example doubling or tripling. Multiplying by 2 stretches the line by a factor of 2.

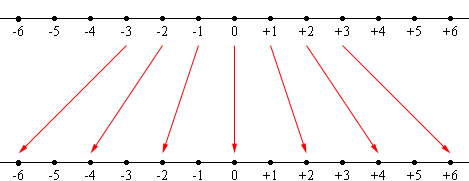
Multiplication by 2

Likewise multiplication by 3 is the action that stretches the line by a factor of 3. You can even extend this to fractions where multiplication by a fraction less than 1 is a contraction of the line.

What about multiplication by -2? We know that -2 × 0 = 0, -2 × 1 = -2, -2 × 2 = -4, -2 × 3 = -6 so there is again a stretching by a factor of 2 but the direction of the line is reversed.

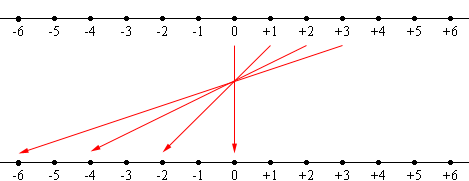
Multiplication by -2

Under this action of stretching by 2 and reversing the direction what happens to the negative numbers?

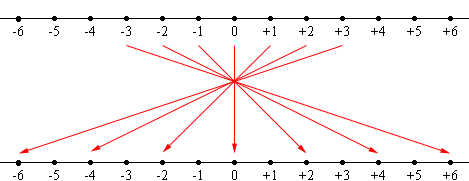
Multiplication by -2

-2 × -1 = +2, -2 × -2 = +4, -2 × -3 = +6 and so on.

This interpretation of multiplication might not seem particularly applied or natural, but is is. It supplies the foundation for building a mathematical model of the motion of an object along a line or even the motion of an object in 3-space.

This example comes from Barry Mazur's book Imagining Numbers (particularly the square root of minus fifteen).

I hope this helps,
Harley