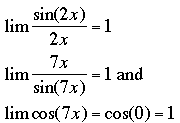| |||
| Math Central | Quandaries & Queries |
|
Question from Teri, a student: Although I have this problem completely worked out in front of me I still cannot understand |
Hi Teri,
The key here is
What this says is that if you have the sine of some expression divided by the same expression and you take the limit of this fraction as the expression goes to zero, the value is 1. In your problem you have both sin(2x) and sin(7x) and I would like to make them sin(2x)/2x and sin(7x)/7x so that I have the sine of an expression divided by the same expression. This is what I do
What I did was divide sin(2x) by 2x to get "the sine of some expression divided by the same expression", perform the same trick with sin(7x) and then to maintain the equality I needed to multiply by (2x)/(7x) = 2/7. Now when I take the limits I get
Thus the final value is
1 × 1 × 1 × 2/7 = 2/7.
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.