| |||
| Math Central | Quandaries & Queries |
|
Question from Thejas, a student: A regular hexagon is inscribed in a circle. If the perimeter of the hexagon is 42 inches, how many inches are in the circumference of the circle? |
Thejas,
The perimeter of the regular hexagon is 42 inches so each side has length 42/6 = 7 inches.
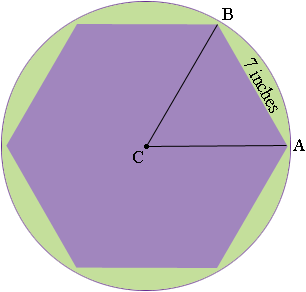
The measure of angle BCA is 360/6 = 60o. CA and CB are radii of the circle so triangle ABC is an isosceles triangle. What is the length of CA?
Penny
Thejas,
(1) Draw an accurate sketch, including the circle, the hexagon, and the long diagonals of the hexagon, and you should be able to guess how the radius of the circle relates to the perimeter of the hexagon. To prove this, use symmetry and the fact that a regular hexagon has angles of 120 degrees and a regular (equilateral) triangle has angles of 60 degrees.
(2) Now use the usual formula C = 2 π r for the circumference.
Good Hunting!
-RD
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.