| |||
| Math Central | Quandaries & Queries |
|
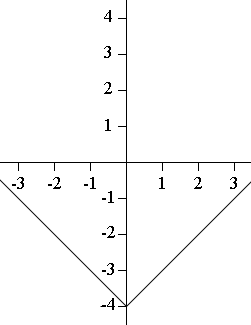
Question from tiana, a student: how do you find where to plot Y in a problem that states y=|x| -4? |
We have two responses for you
Tiana,
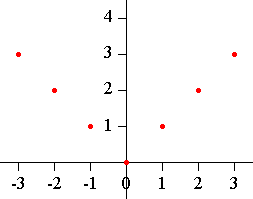
I would first plot some points to sketch the graph of y = |x|.
Make a table
| x | y = |x| |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| -1 | 1 |
| -2 | 2 |
| -3 | 3 |
plot the points
sketch the graph.
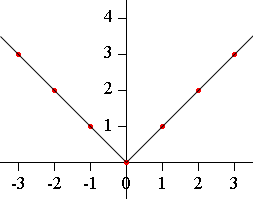
y = |x|
For the function y = |x| - 4 each y-value is 4 less than the corresponding y-value for y = |x|.
y = |x| |
y = |x| - 4 |
I hope this helps,
Penny
Two possibilities:
(1) The brute force method, on which everybody has to fall back sometimes, is to choose a lot of values of x, compute |x| and then |x| - 4 for each of them, and plot the point. Then draw a curve through the points. It helps to know that the absolute value function, unlike most others, really does yield a graph with a "kink" in it; it is thus an exception to the usual situation when a smooth curve is appropriate.
(2) By transformation: if you know what the graph of y=|x| looks like (and it is useful to know), you can lower it 4 units to get the graph you want. You can use the same technique to plot things like y = sin(x) +3, y = x^2 - 1, etc.
Good Hunting!
-RD
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.