Water drains from a conical tank

HOME

Math Central

Quandaries & Queries

Question from Tyler, a student:

Water drains from a conical tank at the rate of 5ft/min^3. If the initial radius of the tank is 4' and the initial height is 10'.
a) What is the relation between the variables h and r? (height and radius)
b) How fast is the water level dropping when h=6'?
Thanks for the help, i'm stumped.

Hi Tyler,

I assume h and r are the height and radius of the water in the tank in feet at some time t minutes. The tank it self has a radius of 4 feet and a height of 10 feet.

tank

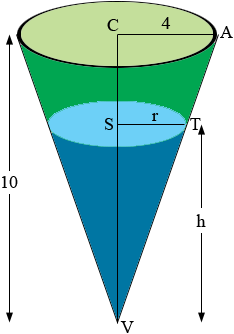
In the diagram the triangles ACV and TSV are similar and hence

4/10 = r/h.

The volume of water in the tank at time t is

V = 1/3 π r² h cubic feet.

Use the relationship between r and h above to write V in terms of h alone. Differentiate this function with respect to t. Use the fact that dV/dt = 5 ft³/min to find dh/dt when h = 6 feet.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.