| |||
| Math Central | Quandaries & Queries |
|
Question from Wanda, a parent: One boy holds a yardstick vertically at a point 40 feet from the base of the flagpole. The other boy backs away from the pole to a point where he sights the top of the pole over the top of the yardstick. If his position is 1 ft 9 in from the yardstick and his eye level is 2 ft above the ground, find the height of the flagpole. |
Hi Wanda,
Did you draw a diagram?
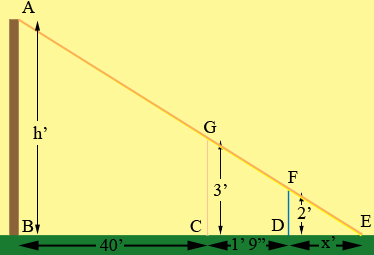
The second boy's eye, the top of the yard stick and the top of the flagpole form a straight line. I extended this line to meet the ground at E and called the distance the second boy to the ground |DE| = x feet.
The triangles GCE and FDE are similar and hence
|CE|/|GC| = |DE|/|FD|
(1' 9" + x')/3' = x'/2'
But 1' 9" = 1.75' and hence you can solve the above equation for x.
Now use the fact that triangles ABE and FDE are similar to find h.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.