Hi Anna.

You should start by drawing a diagram. Here's mine:

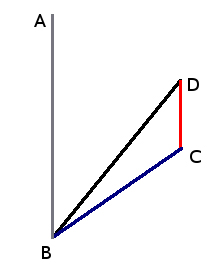
The point B is the starting point for the plane. The line AB is true Northwards. The plane is heading towards D, so angle ABD is 40 degrees because the plane aims for 40 degrees east of north. That means the black line BD represents the planes path in the air; its length is 180. The red line DC is the south-bound wind so its length is 35. Since the wind DC is parallel to AB, that means the angle ABD is the same as angle CDB. So in the triangle BCD, you know the lengths of two sides and also the included angle between them.

You want to find the direction of BC, the direction of the plane with respect to the ground. In fact, you want to know the size of angle ABC.

Here's one way to do it:
1) Use the Law of Cosines to find the length BC. Since you know BD and DC and angle BDC, you can find BC.
2) Now that you know BC, BDC, and DC, you can use the Law of Sines to find the size of angle BCD.
3) The answer is just 40 degrees (the size of ABD) plus the result of step 2.

If you aren't sure about using the Law of Cosines or the Law of Sines, you can look those terms up in our Quick Search - you'll see lots of examples in there.

Cheers,
Stephen La Rocque.