Hi Debbie,

I assume you mean there is one juice box per person and each package holds 3 juice boxes. Since there is 27 people (25+2=27) and 3 juice boxes, there is a need for 9 packages because 27/3=9. In this case, all the juice boxes will be used up from the 9 packages but what if there was a different number of people?

Let's assume there was 24 students and 2 teachers. Now there 26 people instead of 27 but 9 packages of juice will still be needed because 26/3 = 8.67. We can only use whole number amounts of packages so we always round up to the next integer, in this case 9.

Understanding conceptually how many packages of juice boxes we need helps us determine if our answer is reasonable but it does not determine an array. Let's get rid of the assumption that there will only be one juice box per person. We know we need a minimum of 27 juice boxes (j) or j ≥ 27. Since there are always at least three times as many juice boxes as packages (p) needed so j ≥3p. If we graph these two constraints, we get the following area of intersection:

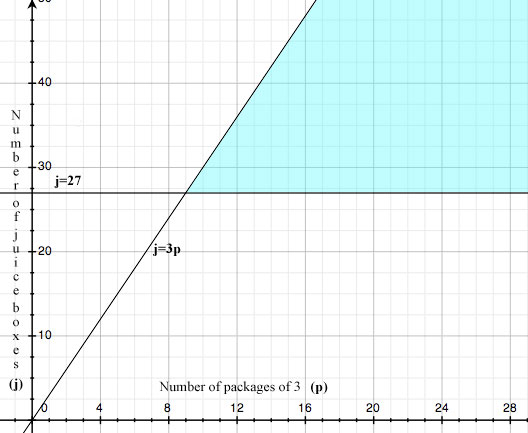
Any intersection points are an optimization or this case the minimum number of cases needed for the group of 27.

From the constraints j ≥ 27 and j ≥3p (or j-3p ≥0) we can create the array Ax≥b where

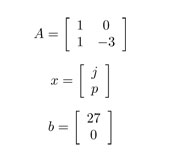
Hope this helps,

Janice