| |||
| Math Central | Quandaries & Queries |
|
Question from Jim, a student: Hello I have a hard time finishing this question: A right circular cylinder has to be designed to sit inside a sphere of radius 6 meters |
Hi Jim
Using the information you gave me, I came up with the following diagrams
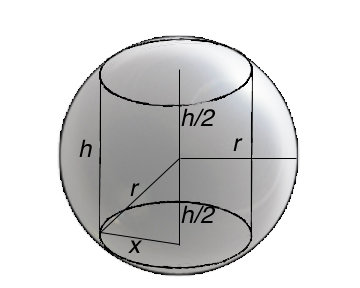
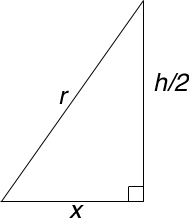
The volume of the cylinder is V=πx2h. The radius of the sphere and the radius of the cylinder's base form a triangle with the height of the cylinder. Using the Pythagorean Theorem we can say x2+(½ h)2=r2
Using implicit differentiation with respect to x, we arrive at the following
| dV/dx = 2πxh + πx2dh/dx | 2x+½ h dh/dx = 2r dr/dx |
Since the radius is not changing dr/dx = 0
2x+½ h dh/dx = 0
You can now solve for dh/dx from the above equation and substitute it into the change of volume formula
dh/dx = -4x/h
dV/dx = 2πxh + πx2dh/dx= 2πxh + πx2(-4x/h)
At minimum or maximums, rates of change equal zero. So for the maximum volume dV/dx=0
0 = 2πxh + πx2dh/dx= 2πxh + πx2(-4x/h)
You can now solve for x in terms of h then use the Pythagorean Theorem to find the dimensions of your maximum cylinder.
Hope this helps,
Janice
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.