Hi Mark,

Let's look at your information in terms of the quotient and remainder. If we multiply the quotient by a number and add the remainder we will get the desired unknown integer. So we get

x=qn+r

where x is the unknown integer, q is the quotient, n is an integer and r is the remainder.

In your case,

x = 7n + 4

x = 8m + 5

x = 9p +6

Since 7, 8 & 9 can all be multiplied by different integers it isn't as simple as solving an equation. The easiest but most time consuming way to determine your integer would be setting up a spreadsheet with these equations

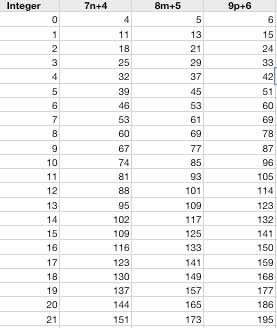
It will take some time to look through the list to find a number that is common to each column and you may have to generate a lot of numbers before you find one (I had to generate about 150 numbers for each column before I found an answer using this method).

A quicker way to generate the list would be generating two columns instead of 3. For example we know

7n+4=9p+6 and 8m+5=9p+6

If we solve both of the equations for p

p=(7n-2)/9 and p=(8m-1)/9

When you generate you list you only have to look for the whole number answers

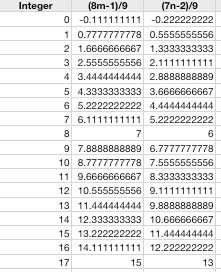
The whole numbers represent values that are multiples of 9. I still generated just as many numbers as the previous list but there are much fewer numbers to compare. Once you find an integer that is common to both columns, you have your value of p and can easily determine your needed number.

Hope this helps,

Janice