Hi Tamara,

I am going to assume a certain level of knowledge of Newton's Laws. We need to use the formula for density (mass per volume) and pressure (force per area):

ρ = m/V which can be written as

Vρ = m or Ahρ = m

where ρ is density, m is mass, V is volume, A is area and h is the height (or in this case the depth of the water).

P = F / A which can be written as PA = F

where P is pressure, F is force and A is area.

If we look at the free body diagram for the situation

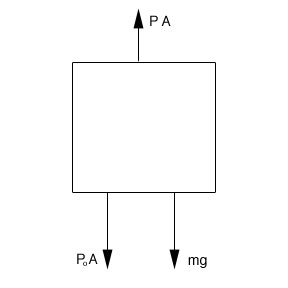
P_o is atmospheric pressure which is approximately 1.013 x 10⁵ Pa at sea level. P is the pressure for the given density and depth and g is the acceleration due to gravity. There will be the force from the atmospheric pressure as well as the weight "pushing" the object down. The pressure from the water is "pushing" the object up. Since the object is not moving:

PA – mg – P_oA = 0 since we already determined Ahρ = m

PA –Ahρg – P_oA = 0 since all of the terms have A, we can cancel it.

P –hρg – P_o = 0

P= hρg +P_o

Now you can quite easily solve for pressure.

Hope this helps. Make sure to write back if there are any steps you don't understand.

Janice