Allan,

You can construct many different triangles with different heights on a base that measures 2.4 meters. Below are 10 triangles of different heights on a base of 2.4 meters.

Do you know anything else about the triangle?

Penny

Allan wrote back

Dear Penny,The top internal angle will be 90 degrees

Allan,

This is still not enough information to determine the height of the triangle.

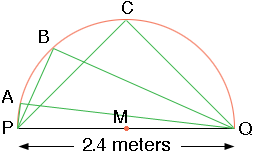
In my diagram M is the midpoint of the base PQ. I then drew a semicircle with center M and radius 2.4/2 = 1.2 meters. If you take any point on the semicircle, for example B in my diagram, the the triangle BPQ has an angle of 90 degrees at B. This is a theorem of Euclid.

If the point you choose on the semicircle is C, half way around, then the height of the triangle CPQ is 1.2 meters. You could however chose the point on the semicircle to be A, very close to P, and then the height would be very close to zero. The point B on the semicircle can be anywhere between A and C so the height of your triangle could be any number between 0 and 1.2 meters.

I hope this helps,
Penny