Hello,
A good place to start is with a picture:

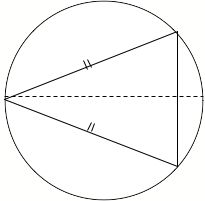
Consider the circle to be centred at the origin of the Cartesian plane.  In other words, it has equation:

x² + y² = 16

We want to maximize the area of this triangle so we would like a formula for such; for that we consider splitting this picture on its axis of symmetry (dotted line above).  If we let  y  be half the length of the base then the area of the triangle is given by:

Area = (x + 4)y for -4 ≤x ≤ 4

We have the condition that the triangle is inscribed in the circle, therefore if we solve for   y   in the first equation and substitute into the second we obtain:

Area = (x + 4) √(16 - x²)

We wish to maximize area, thus we take the derivative of this formula then set it equal to zero and solve to find the critical points of the function.  Are these max or min values?  Use the Second Derivative Test to confirm.  Are they absolute maxes or mins?  What is the absolute max for area?

For the other question, the words volume and surface area are mentioned, therefore we will probably benefit from knowing formulae for these.  The shape is composed of two hemispheres and a right circular cylinder, therefore the volume of the solid is:

V = 2(Volume of a hemisphere) + (Volume of a cylinder)

V = (Volume of a sphere) + (Volume of a cylinder)

What are the formulae for these solids?
The surface area is then given by:

S.A. = 2(Surface area of a hemisphere) + (Surface area of a cylinder)

S>A> = (Surface area of a sphere) + (Surface area of a cylinder)

What are the formulae for these?
We are given that   V =  12, therefore we can use the volume formula to eliminate variables in the surface area formula to obtain a formula in terms of radius only.
We wish to minimize this formula.  Proceed by analogy with the method of the previous question.

Hope this helps,
Tyler