Hi Amper,

You have real numbers a and b and for any positive real number x, a is less than or equal to b + x. The possibilities for the relationship between a and b are a < b, a = b and b < a.

Can it be that a = b? For example can a = b = 5? Yes! If a = b = 5 then for any positive real number x, b + x = 5 + x > 5. So not only is 5 less than or equal to 5 + x it's actually less than 5 + x. This is part (b) of your problem.

Hence for the three possibilities of the relationship between a and b, a < b, a = b and b < a, I know that a = b is a valid possibility.

Can b be less than a? On the number line this would be

But if I then took x to be half the distance between a and b I would have

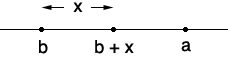
which says b + x < a which is impossible since I know that a is less than or equal to b + x.

What I just showed you is a sketch of a proof of (a) by contradiction. You need now to write it carefully. Assume b < a and prove carefully that b + x < a which is a contradiction.

I hope this helps,
Penny