Amroziz,

The graph of y = x is a straight lie through the origin at an angle of 45^o with the positive X-axis. The graph of y = 2 sinx is periodic around the X-axis with an amplitude of 2. Hence the graph of f(x) = x + 2sinx oscillates around the line y = x. Here is its graph (the X-axis is in radians).

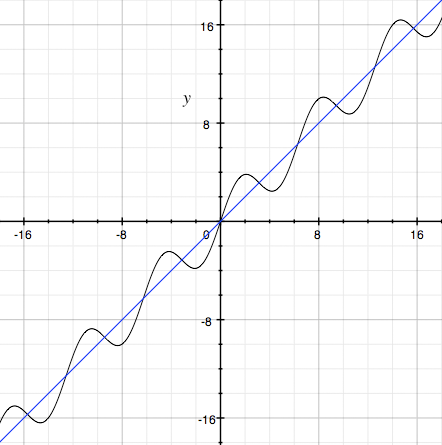
As you can see there are infinitely many points where the graph has a horizontal tangent. To identify these points find the derivative f'(x) of f(x) with respect to x and solve f'(x) = 0. You should find two values of x with 0 ≤ x ≤ 360^o. The complete solution is then these values plus or minus an integer multiple of 360^o.

Harley