Sure Austin.

The "intersection" is where both functions have the same (t,y) variable values.

This means that the y in the first function is the same as the y in the second function. Of course you know that if something1 = y and y = something2, then something1 = something2.

So

-4t + 300 = -4.9 (t - 5)² + 300

Now you can simply solve for t using any of the quadratic techniques (factoring, completing the square, quadratic formula...).

-4t = -4.9 ( t² - 10t + 25)

-4t = -4.9t² + 49t - 122.5

4.9t² - 53t + 122.5 = 0

This job is clearly one for the quadratic formula. Remember it looks like this:

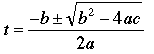
The "t" is the unknown, but a, b, and c are the co-efficients in front of the squared, linear and constant parts. That is, a = 4.9, b = -53 and c = 122.5. That means we substitute these in:

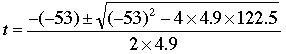
And using a calculator, we calculate that there are two values of t (because of the plus/minus): 7.47 and 3.35. I'm guessing that these are seconds, because your question looks like it is modelling motion under the influence of gravity over time.

The last step is this: for EACH value of t you just plug it into the easier formula you started with to calculate y.

y = -4(7.47) + 300 = 270.12
and
y = -4(3.35) + 300 = 286.60

And so the intersection points are (t,y) = (7.47, 270.12) and (3.35, 286.60).

Hope this helps,
Stephen La Rocque