| |||
| Math Central | Quandaries & Queries |
|
Question from avien, a student: a rectangle has a line of fixed length L reaching from the vertex to the midpoint of one of the far sides. what is the maximum possible area of such a rectangle? SHOW SOLUTION USING CALCULUS |
Avien,
Suppose the sides of the rectangle are of length x and y.
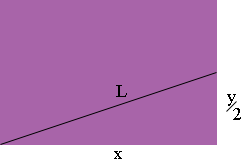
The area of the rectangle is
area = xy square units.
Look at the diagram. What does Pythagoras theorem tell you about the relationship among x, y and L? Use this to write the area as a function involving only x and L. L is fixed (a constant) so you can use the calculus you know to find the value of x that maximizes the area.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.