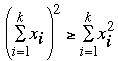 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Bhavya, a student: Prove by induction that if Xi >= 0 for all i, then (Summation Xi from 1 to n)^2 >= Summation Xi^2 from 1 to n |
Hi,
First I suggest that you look at Victoria's response in The Principle of Mathematical Induction.
For her step 1. check that your statement is true for i = 1.
Step 2. assume that your statement is true for some n = k ≥ 1. Thus for your statement that is assume that for some k ≥ 1
Step 3. is the inductive step. Based on the assumption in step 2. you are to prove that
(*).
To prove this let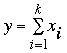 
then the left side is (xi + y)2. Expand this using the binomial theorem and use the assumption in part 2. to conclude that statement (*) is true.
Perform step 4.
I hope thus helps,
Penny
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.