| |||
| Math Central | Quandaries & Queries |
|
Hello, i am a freshman at Monona Grove high school. this is a question that was on a test at a math competition i want to last year in 8th grade. i have been working on this problem periodically for the last 9 months. i even asked both my math teachers (one geometry and the other algebra 2), and neither of them knew how to solve it either. i also asked another freshman at my school who is in calculus(and taking classes at a college next year!!!) who is like really smart, and he was stumped. during the competition, i got the answer right, just by guessing, but i really want to know how to SOLVE the question, because now i feel bad because i won the award for highest score out of like 250 students. i feel like i won because i guessed, and that doesn't seem fair. My Question: There is a quarter circle with a radius of 1. along one edge of it, there is a semicircle with a diameter of 1, and its center is on the drawn line. there is another semi-circle again with the center on the other drawn line, and this one has an unknown diameter of X. both circles are internally tangent, and are tangent to each other. Find X. i have included an attachment of the problem. the reddish dots are points of intersection. |
Brandon's diagram
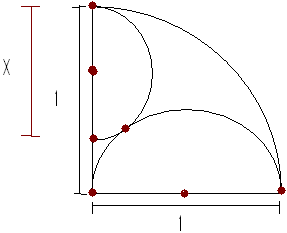
Brandon,
Your picture is wrong! There is a theorem you are overlooking: When two circles are tangent then the line joining their centers passes through the point of tangency. The Pythagorean theorem then gives an equation for x.
Chris
Brandon,
Look carefully at your diagram. Do you see anything suggesting a line that is not currently there? Add it.
Now label all radii of [semi,quarter]circles that you can find. Label the radius of your unknown semicircle "x".
Look for a right triangle whose sides you know, at least in terms of "x". Use Pythagoras.
Good Hunting!
RD
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.