Bruce,

            Although I will address your query at the end, it is best to begin with convex polygons.  Otherwise, a polygon can be a very general object — it consists of vertices and edges; the vertices do not have to lie in a plane, nor must they be finite in number.  The definitions: Vertices are points that have been labeled in order 1, 2, 3, ... , and edges are the line segments that join vertex number j to vertex number j+1.  A polygon with n vertices is called an n-gon.  In general, the edges can cross; vertices can be collinear and are even allowed to coincide.  On the other hand, for an n-gon to be convex each of its n edges must lie on a line that contains the successive vertices that define it, and the other
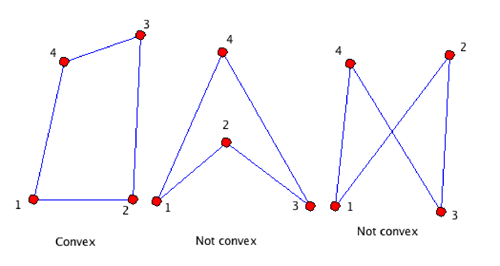
n – 2 vertices must all lie in the half-plane on one side of that line.  For both of the nonconvex quadrangles in the accompanying figure, vertices 3 and 4 are on opposite sides of the line joining vertices 1 and 2.

            We will find it convenient to use directed angles.  An angle at the vertex j is the measure of the angle through which ray directed from vertex j to vertex j+1 must be rotated about vertex j in the counterclockwise direction to point in the direction from j to j-1 (where we consider the last vertex n to be the same as 0): 

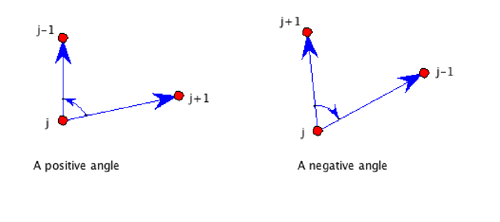
With this definition, if we label the vertices of a convex n-gon in the counterclockwise direction, all the angles are positive numbers less than 180 degrees.  Compare that with the middle quadrangle in the first figure: one must decide whether to call the angle at vertex 2 negative, or greater than 180 degrees.  (If we define it to be negative, then the sum of the angles of that quadrangle will be zero; if the angel at 2 is defined to be greater than 180 degrees, then the angle sum will be 360.)  For the nonconvex quadrangle on the right, the only interpretation that makes sense to me is for the angles at vertices 2 and 3 to be negative, and at 1 and 4 to be positive, in which case the sum of the angles of that quadrangle will be zero. 
            So let us now work with a convex n-gon.  There is a simple way to determine its angle sum.  I shall give the argument for the pentagon ABCDE shown below, but you

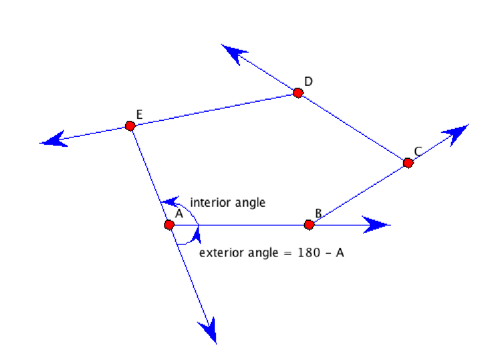
should easily see how it would work for any n-gon.  Put your pencil on the edge EA pointing from E to A, then rotate it about A so that it lies along AB pointing toward B.  Next, rotate it about B until it points toward C, then about C until it points to D, and so on until you rotate about the last vertex E until your pencil points toward A.  Note that your pencil has made one complete revolution — its turned through an angle of 360 degrees.  (That's why we defined convexity the way we did!)  Next, observe that the angle through which the pencil rotates about each vertex is the supplement of the angle at that vertex (so that it rotates (180 – A) degrees about vertex A, (180 – B) degrees about B, and so on.  Thus the pencil's total rotation is
                 360 = 180 – A + 180 – B + 180 – C + 180 – D + 180 – E
                        = 5 · 180 – (Angle sum).
It follows that the sum of the angles of the pentagon ABCDE is
                        Angle sum = 5·180 – 360 = 3·180 degrees.
In general, this argument applied to an n-gon will tell you that the sum of the interior angles of a convex n-gon is (n – 2)·180 degrees.
            Now we are ready to look at your questions.  If an interior angle of your convex n-gon is 90 degrees, then so is the exterior angle.  For your pencil to rotate 360 degrees as it moves around the outside, it can go through at most four right angles (in which case there could be only 4 vertices and the 4-gon is a rectangle).  When n is greater than 4, then there could be at most three right angles; all the other n – 3 exterior angles would have to add up to the remaining 90 degrees (so that the remaining interior angles would each have to be bigger than 90 degrees). 
            Finally, let us consider what might happen when the n-gon is not convex.  When n is even and greater than 2, then a nonconvex n-gon can have a right angle at every vertex — all n angles are right angles.  Imagine walking about a city whose streets form a grid of north-south and east-west streets.  If you start walking east (as shown with the accompanying 8-gon),

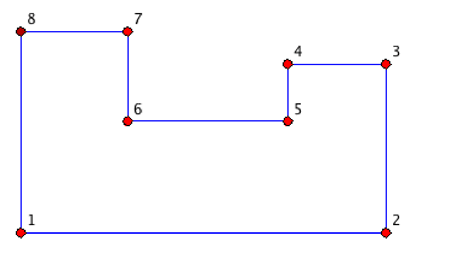
you can end up back at your starting point after an even number of turns (either right or left) as long as your last turn is taken at a point due north or due south of the starting point.
            Finally, when n is odd then a nonconvex n-gon can have n – 1 right angles: since n is odd, n – 1 is even, so you can draw an (n – 1)-gon with n – 1 right angles.  Now put a new vertex on any one of those n – 1 edges and you will have an n-gon with n – 1 right angles and one angle of 180 degrees.  (If you do not like an n-gon to have collinear vertices, then draw a figure with n – 2 right angles starting at some point 1 and ending at point n, n odd, then join point n to point 1.  The angles at n and at 1 will not be 90 degrees because, using the street analogy again, after an even number n – 1 of right turns you would be walking parallel to the first street you walked down.) 

Chris