Bruce,

The volume of the space remaining in the tank is the cross-section area of the remaining space (shaded green in the diagram) times the length of the tank, which you know is 72 inches.

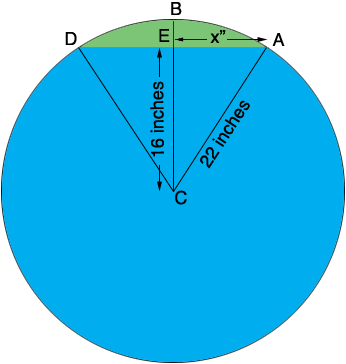
The cross-section area of the space remaining is the area of the sector CABD minus the area of the triangle ADC. To find the area of the triangle I used Pythagoras theorem do calculate x. Pythagoras theorem says

22² = 16² + x²

so

x = √(22² - 16²) = 15.1 inches.

Hence the area of the triangle ADC is 15.1 × 16 = 241.6 square inches.

Next I used trigonometry to determine the angle ECA. cos(ECA) = 16/22 = 0.7273 and hence the measure of angle ECA is cos^-1(0.7273) = 43.341 degrees and hence the measure of the angle DCA = 86.684 degrees. All the way around the circle is 360 degrees so the angle DCA is 86.684/360 = 0.24079 of the way around the circle. By the symmetry of the circle the area of the sector ABDC is 0.24079 of the area of the circle. Thus the area of the sector is

0.24079 × π × 22² = 366.1 square inches.

Hence the area of the cross-section region is 124.5 square inches. Finally the volume of the space remaining in the tank is 124.5 × 72 = 8966.2 cubic inches.

All that remains is to convert this to gallons and Google can help here. Type 8966.2 cubic inches in gallons into the Google search window and Google responds with 8 966.2 (cubic inches) = 38.8147186 US gallons.

Harley