| |||
| Math Central | Quandaries & Queries |
|
Question from Charlene, a student: The ratio of the width to the length of a certain rectangle is equal to the ratio of its length to the difference between its length and twice its width. If the area of the rectangle is 25cm^2, then what are its dimensions? Present a non- algebraic solution? |
Hello,
Let w be the width, and l be the length of the rectangle.
The information given amounts to stating that:
Where |l - 2w| is the absolute value of the difference between the length and twice the width.
(Both w and l are positive numbers, so it doesn't make sense for (l - 2w) to be negative if the second equation is to be satisfied)
Therefore we have two cases:
Case 1 Solve for w and l given:
Case 2 Solve for w and l given:
You will find that one case is not possible.
For a non-algebraic solution, consider a line segment divided up as such:
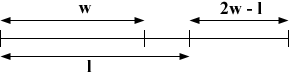
The length of w is to l as length of l is to 2w – l ?
How long does 2w – l have to be for our equation to make sense?
Hope this helps,
Tyler
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.