Hi Chip,

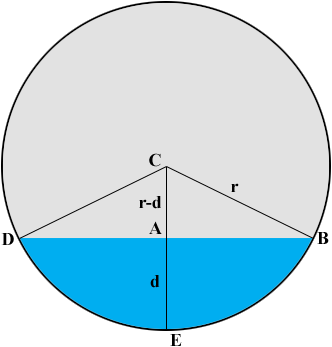
You know r and d in the diagram. I'm going to calculate the area of the cross section of the water as the area of the sector CDEB minus the area of the triangle CDB.

Triangle CAB is a right triangle so useing Pythagoras theorem

(r - d)² + |AB|² = r².

Solving for |AB| gives

|AB| = √(2rd - d²).

Now you can calculate the area of the triangle CDB using the fact that the area is one half the base times the height.

Looking at triangle CAB again I see that cos(angle BCA) = (r - d)/r and hence the measure of angle BCA is cos^-1[(r-d)/r]. (When using your calculator to find cos^-1 make sure it is set on degrees.) Hence the measure of the angle BCD is given by θ = 2 cos^-1[(r-d)/r].

This angle is a fraction of one entire revolution of the circle, in fact it's θ/360 of the way around the circle. By the symmetry of the circle the area of the sector CDEB is θ/360 of the area of the circle. That is

area of the sector CDEB = (θ/360) × π r².

I hope this helps,
Penny