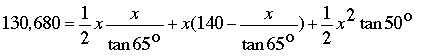Cliff,

No, you do not have enough information. If you make one of the edges next to the known one a few feet long and the fourth edge parallel to the known one, the area will be only a few hundred square feet. Now swing the edge around so it's nearly parallel to the opposite edge; the new area is huge. Somewhere in between you would have had the right area and satisfied all your conditions. But (apart from being fairly short) the length you picked was arbitrary.

Good Hunting!
RD

Cliff wrote back

Let me try again.
If I have a property line that is 140 feet long from left to right and on the left end had a line with an angle of 65 degree's and on the right end had a line with an angle of 140 degree's. How far out those two lines would you have to go to get 130,680 square feet, by making the connecting line parallel to the 140 foot line?

Hello Cliff,
Is this the layout of the property you are trying to figure out?

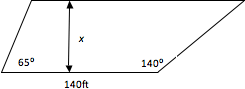
We would like an equation for the area of this figure, and for it to only involve the variable, x, the distance between the two parallel sides.  Let’s add some extra perpendicular lines, and some variables.

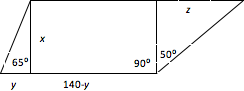
From our new picture, we have the following equation for the area of this entire figure:

Area =

We can eliminate the extra variables using some knowledge of trigonometry:

tan 65^o = x/y and tan 50^o = z/x

Which means that, y = x/tan 65^o and z = x tan 50^o. Substituting these into our area equation, and setting area to 130,680 square feet we get:

After simplification, you can solve the resulting quadratic equation for x.
Write back if you have more questions.

Tyler