| |||
| Math Central | Quandaries & Queries |
|
I live in St. Joseph, Michigan and there is an ongoing argument regarding line-of-sight over the horizon. Standing on a 200 foot high bluff here, people swear they can see the top of the Willis (nee Sears) Tower in Chicago, which is about 1653 feet high. It is my contention that this is actually a "refracted reflection" and not direct-line-of-sight. So, to settle the argument, I'd sure like some simple explanation for this, even if-and I hope not-I am incorrect. David |
I David,
I copied Penny's diagram from her response to a similar question.
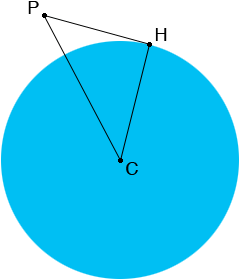
P is the top of the bluff, C is the centre of the Earth and H is a point on the horizon for someone standing at P. The radius of the Earth is about 3963 miles and 200 feet is 200/5280 miles so the length of CH, |CH|, is 3963 miles and the length of PC, |PC|, is (3963 + 200/5280) miles. The angle CHP is a right angle so we can use Pythagoras theorem which says
|PC|2 = |CH|2 + |HP|2
or
(3963 + 200/5280)2 = 39632 + |HP|2.
Solving for |HP| I get |HP| = 17.3 miles.
I then repeated the calculation, this time with P the top of the Willis Tower and got
(3963 + 1653/5280)2 = 39632 + |HP|2.
In this case |HP| = 49.8 miles.
Thus someone at the top of the bluff can see over the horizon to the top of the tower as long as the bluff and the tower are less the 17.3 + 49.8 = 67.1 miles apart.
I then went to Google Maps and asked for a route from St. Joseph to the Willis Tower and used the scale to estimate the distance, "as the crow flies". (I cut and pasted the scale below.)
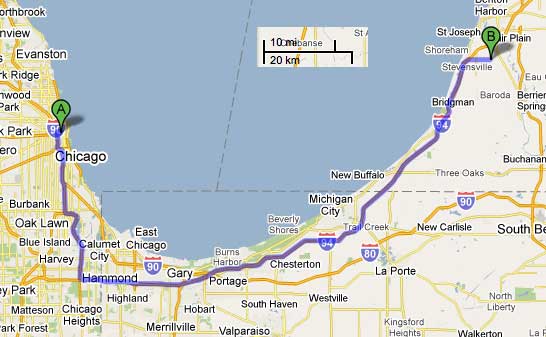
From the map my estimate of the distance is 63 miles.
So who is right? It's quite close. You probably have a better idea of the distance from the bluff to the tower.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.