Hello Emma,
We begin by plotting the two points and drawing the line between them:

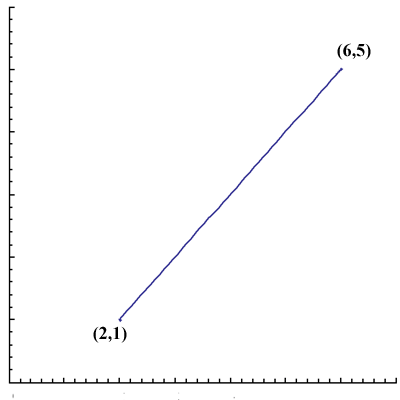
The length of this line segment is  4 √2 (using distance = )

An equilateral triangle is one in which each side is the same length.  Thus we need to find the coordinates of the two points which are at distance 4 √2  from both (2,1) and (6,5).  We will do this using the ‘ruler and compass’ construction of equilateral triangles:

Draw two circles of radius 4 √2  having centres at (2,1) and (6,5).

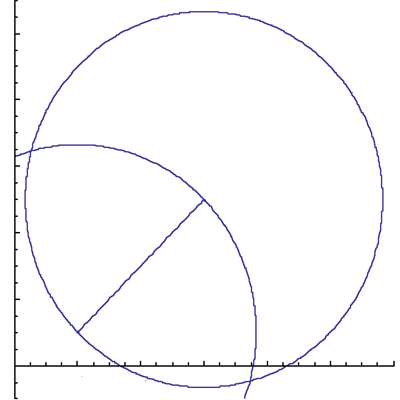
Where the two circles intersect  are the desired coordinates needed as vertices for our equilateral triangle.  How do we find these coordinates?  Formulae for these circles would be handy.

A circle of radius r with centre (h,k) has formula,

Since you have two circles, you get two equations in two unknowns, and you can solve for the coordinates.

*There is also an easier way using the perpendicular bisector of the original line segment.  Can you see how?
Tyler