| |||
| Math Central | Quandaries & Queries |
|
Question from Frank: I'm not sure if this is a proper question to ask so if I have misdirected my question I apologize and no response is expected. I am trying to figure out a way to measure vapor trails from my back yard in Phoenix Arizona. If I used a compass and spread each point of the compass to the start and finish of the vapor trail I would have the angle of an isosceles triangle. The other two angles would be identical. The height of from the inverted base of the triangle to my standing spot on the ground would be about 35,000 feet. I'm thinking that there should be a way to figure out the length of the inverted base (vapor trail) but I'm devoid of mathematical skills and can't seem to figure out how to do this. Is it possible to figure out the length of a vapor trail using this method or do you have an easier way to accomplish the task? Any help you could offer would be most appreciated. Thanks....Frank |
Hi Frank,
Here is how I see the situation you describe. Frank is at point F and the vapors cover the triangle FAB. I let C be the midpoint of AB so the distance from F to C is approximately 35,000 feet and you want to find the distance from A to B.
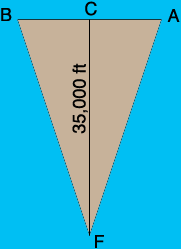
Since C is the midpoint of AB the angle ACF is a right angle. Suppose the angle CFA has measure t degrees then
tan(t) = |AC|/|CF| = |AC|/35,000
and hence
|AC| = 35,000 tan(t)
and
|AB| = 2 × 35,000 tan(t) = 70,000 tan(t).
You told us that you used a compass to find the bearings of A and B from F so that will allow you to determine the measure of the angle BFA and half of that is t.
I am not sure how accurately you can measure the length of |CF| and the bearings of A and B. Measurement errors in these quantities will result in inaccuracies in the calculation of |AB|. For example if you think the length of |CF| is 35,000 ± 1,000 feet and you think you know t within ± 5o then perform the calculation with |CF| = 34,000 ft and 36,000 ft and with t varying by ± 5o and see how the resulting value of |AB| changes.
Good luck with this,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.