A question from a boat builder

HOME

Math Central

Quandaries & Queries

Question from Grant:

I am a boat builder, trying to lay out shape of side's elevation.
My question is, how do I define the length of a circle's radius, if I know the chord length
(20 ft) and the segment of the radius between the chord and the circle is known (7 inches)?

Grant,

Is this the situation you are describing?

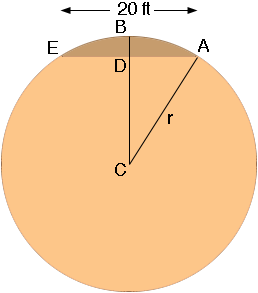
chord and arc

The chord EA is 20 feet long, D is the midpoint of the chord and the distance from B to D is 7 inches. If this is the correct diagram then the distance from A to D is 240/2 = 120 inches and the distance from D to C is r - 7 inches. The triangle ADC is s right triangle so Pythagoras' theorem tell us that

|AD|² + |DC|² = |CA|²

and hence

120² + (r-7)² = r².

Expanding gives

14400+ r² - 14r + 7² = r².

Solving for r I get

r = 14449/14 = 1032.07 inches.

Let me know if I have misinterpreted your question.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.