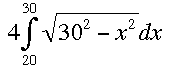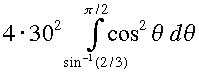We have two responses for you.

Hello Hayden,
Let’s draw a picture of the situation:

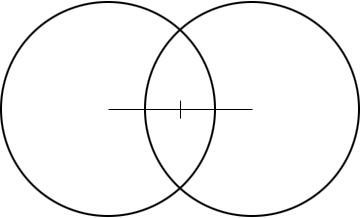
Since the circles have radius  r = 30 ft, and their centres are  40 ft apart, the point where they intersect (the dash in the line above) is at 20 ft. (How do we know this?)

To find the overlapping area, we will use integral calculus.  The problem amounts to finding the value of the integral,

We solve this using a trigonometric substitution: Let x = 30 sinθ and dx = 30 cosθ dθ, and

. Our limits of integration also change, and we have the equivalent integral,

Which can be solve using the half angle identity for cos²θ.

Hope this helps,
Tyler

I am going to use Tyler's diagram but add some lines and labels.

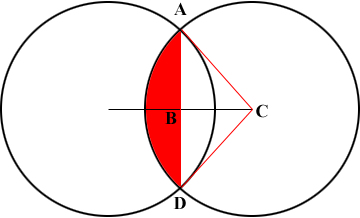
|CA| = 30 ft and |BC| = 20 ft and hence the measure of the angle BCA is cos^-1(20/30) = 48.19 degrees. Hence the measure of the angle DCA is 2 × 48.19 = 96.38 degrees. This is a little more than one-quarter of the way around the circle so the area of the sector DCA is a little more than one-quarter of the area of the circle. More precisely the area of the sector DCA is

(96.38/360) × π × 30² square feet.

You know the lengths of two sides of the right triangle ABC so you can use Pythagoras theorem to find the length of the third side, AB. With this information you can find the area of triangle ABC and then double it to find the area of the triangle DCA.

Finally the area of the region shaded red in the diagram is the area of the sector DCA minus the area of the triangle DCA. This region is one-half the overlap.

Harley