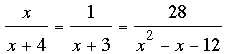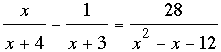Hi Ingrid,

The expression

is actually three equations

, and .

x² - x - 12 = (x + 3)(x - 4) and hence two fractions in final equation in the line above can be written with a common denominator by multiplying the numerator and denominator of the left side by (x - 4). Since the denominators are equal the numerators must be equal and hence

x - 4 = 28

and thus

x = 32.

Substitute x = 32 into the other two equations. If the equations are all satisfied then x = 32 is the only solution. If one of the equations is not satisfied by x = 32 then there is no solution.

Penny

We received a reply

I do apologize for a slight problem with my posting. After the first equation it was suppose to be a minus sign not an equal sign. Now I'll re-post my question. Thanks.

What is the solution set of the equation x over x plus 4 - 1 over x plus 3 = 28 over x to the 2nd power - x - 12 ? Looking forward to a response.

So the equation is

My approach is to look for a common denominator. Since x² - x - 12 = (x + 3)(x - 4) the common denominator I would use is (x + 3)(x - 4)(x + 4). Writing each fraction with this denominator and simplifying leads to

x³ - 2x² - 40x - 96 = 0.

I didn't see any obvious solution so I asked Wolfram Alpha to solve this equation.

I don't think this was the problem you were intended to solve. My guess is that the denominator of the first fraction should be x - 4 rather than x + 4.

Penny