| |||
| Math Central | Quandaries & Queries |
|
Question from Jenny, a student: Two cares are on a collision course toward point P. The paths of the two cars make a 30 degree angle with each other. The first car is 40 km from P, and traveling toward P at 16 km/hour. The second car is 50 km from P, traveling at 20 km/hour. How fast is the (straight line) distance between the two cars decreasing? (Hint: Law of Cosines) |
Hi Jenny,
I drew a diagram and labeled it.
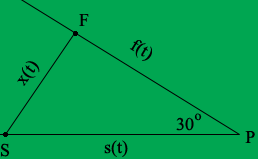
F is the position of the first car and S the position of the second car, both at some time t hours. f(t) is the distance of the first car from P at time t and s(t) is the distance od the second car from P at time t.
Use the Law of Cosines to write x(t)2 in terms of f(t) and s(t). Differentiate this expression with respect to t to obtain an expression of the form
2 x(t) x'(t) = a function of f(t), f'(t), s(t) and s'(t).
At the specific time t* when f(t*) = 40 km and s(t*) = 50 km you can evaluate the right side. Also at t* you can evaluate x(t*) using the Law of Cosines. This then allows you to evaluate x'(t*).
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.