Kapilan,

I am going to illustrate with another function, g(x) = x² - 3.

The technique is to plot h(x) = x² and then look at how the graph changes when you subtract 3.

h(x) = x² is I graph I expect you know.

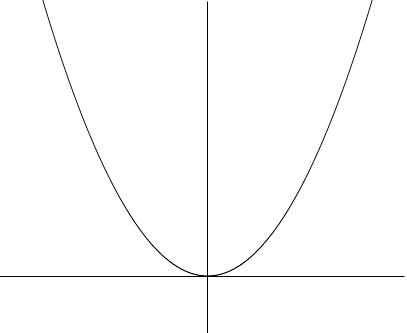
h(x) = x²

Subtracting 3 does not change the shape of the graph but it moves its position on the plane. For the function g(x) = x² - 3 when x = 0, g(x) = -3 and hence the graph passes trough (0, -3). Hence its graph is

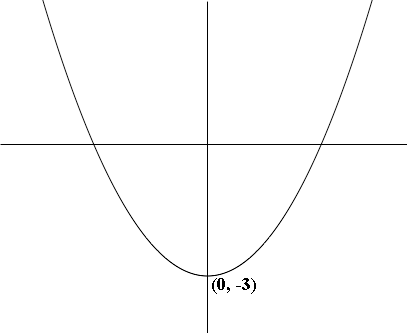
g(x) = x² - 3

What if you change the function h(x) = x² by subtracting 3 from the input to the function, x, rather than the output h(x) to arrive at the function k(x) = (x - 3)²? Again you haven't changed the shape of the function, just where it sits in the plane. Here the vertex of the parabola is at x = 3 and hence the graph is shifted 3 units to the right and becomes

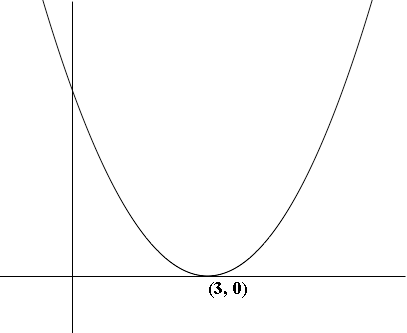
k(x) = (x - 3)²

Harley