I drew a routing diagram from A to C.

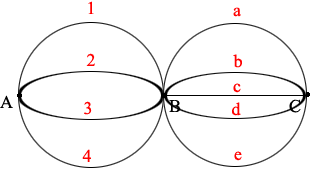
I labeled the 4 routes from A to B as 1, 2, 3 and 4 and the 5 routes from B to C as a, b, c, d and e.

Suppose you take route 1 from A to B then you can continue in 5 ways to get 5 routes from A to C,

1a, 1b, 1c, 1d and 1e.

Suppose you take route 2 from A to B then you can continue in 5 ways to get 5 routes from A to C,

2a, 2b, 2c, 2d and 2e.

Continuing you can see that each of the 4 routes from A to B generates 5 routes from A to C. Hence there are 4 × 5 = 20 routes from A to C.

Each one of these can be extended to a route to D in how many ways? How many routes are there from A to D?

Penny

Kapilan replied

Hi I sent a letter yesterday, Monday Novemeber 30 and I got a reply about my question today. I followed your instructions and typed in routes and found my name, Kapilan. The thing is though the person, Penny did not really help though because what she said I already know and the most
troubling part about the question is the last 2 sentences which she did not quite clear on.

For each of the 20 routes from A to C in how many ways can it be extended to a route from A to D? How many possible routes are there from A to D?

When you arrive at D you have used one route in each of the three legs of the trip. Thus on the way back you have one less route to choose from in each of the three legs.

Penny