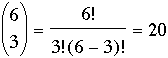| |||
| Math Central | Quandaries & Queries |
|
Question from Kristen, a student: Explain the three different scenarios that could occur and would result in the following number of outcomes when 6 items are taken 3 at a time. Give real-life examples. a. 63 = 6 x 6 x 6 = 216 possibilities b. 6! / (6 - 3)! = 6 x 5 x 4 = 120 possibilities c. 6! / (6 - 3)! 3! = 20 possibilities |
Hello,
Suppose you had 6 different donuts.
If you wanted to know how many ways you could pick 3 donuts with replacement out of 6 you would get:
(# donuts to pick from)(# donuts to pick from)(# donuts to pick from)
= 6 × 6 × 6 = 216.
For instance, I could pick the first donut, then replace it, then pick the first donut again, and replace it, then pick the 5th donut.
If you wanted to know how many ways you could pick 3 donuts without replacement out of 6 you would get:
(# donuts to pick from)(# donuts after 1 is picked)(# # donuts after 2 are picked)
= 6 × 5 × 4 = 120.
If you wanted to know how many ways you could pick 3 donuts without replacement out of 6, and where order doesn't matter (i.e. picking donuts 1, 2, and 3 is the same as picking donuts 2, 1, and 3) you would get:
Division by the factorials removes “equivalent” choices.
Tyler
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.