Hi Luke,

I copied the diagram you sent and added r cm as the radius of the top of the sand in the lower half at time t seconds.

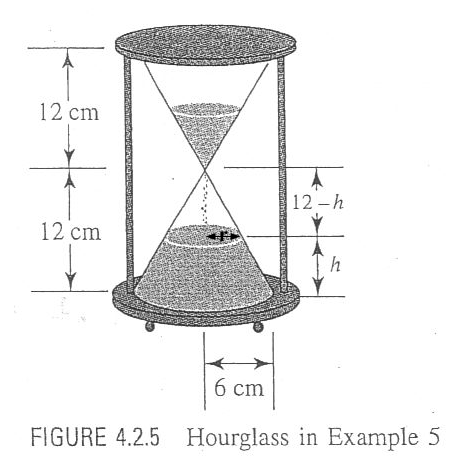
The volume of a cone is 1/3 π R² H where R is the radius of the base of the cone and H is its height. Thus the volume of sand in the bottom half of the hourglass at time t seconds is volume of a cone with radius 6 cm and height 12 cm minus the volume of a cone with radius r cm and height 12 - h cm. If V(t) is the volume of sand in the bottom of the hourglass at time t then

V(t) = 1/3 π 6² 12 - 1/3 π r² (12 - h) = 144 π - 1/3 π r² (12 - h) cubic centimeters.      (1)

You are told that V'(t) = 4 cm³/sec and you want h'(t) at two different times. You can differentiate the expression above with respect to time but the right side will contain h'(t) and r'(t) which doesn't help since you don't have any information of r'(t). The key is the second diagram you sent.

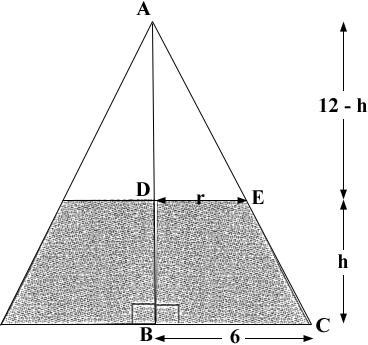
Triangles ABC and ADE are similar so 12/6 = (12 - h)/r. Solve this equation for r and substitute into equation (1). This will give V(t) as a function of h alone. Differentiate this equation with respect to t.

Can you complete the problem now? If not then write back and tell us what you have done and where you are stuck.

Harley

Luke wrote back

Hi Harley,

My name is Luke and I sent you the question concerning the sand in an hourglass. Thank you so much for your help thus far but I'm having problems with my differentiation.

As you stated, I set up a proportion with the similar triangles and found that r=6 - .5h. I then substituted this r value into equation 1 to obtain

V(t)= 144pi -1/3pi(6 - 0.5h)² (12-h).

I tried to differentiate this equation using product rule with chain rule and came up with

-1/3pi(6 - 0.5h)² * -dh/dt + (12-h) * 2(6 - 0.5h) * -0.5dh/dt.

Am I making a mistake with my differentiation thusfar, or do I need to continue and move dh/dt to the left side of the equation? Also, since I know that dV/dt is 4cm³/sec, will I eventually come up with an equation where I can substitute my h values (11cm and 5cm) in and come up with a dh/dt value? Thanks a million!

-Luke

Hi again Luke,

Your procedure is correct but you have an error in the derivative. It's

-1/3pi[(6 - 0.5h)² * -dh/dt + (12 - h) * 2(6 - 0.5h) * -0.5dh/dt].

Harley