| |||
| Math Central | Quandaries & Queries |
|
Question from maelee, a student: hello there, can you kindly answer this question, the official distance between home plate and second base in baseball diamond is 120ft. Find the area of the official ball diamond & the distance between the bases. |
Maelee,
The quadrilateral defined by home plate and the three bases is a square. The line from home plate to second base is a diagonal of the square and divides the square into two isosceles, right triangles. If the distance from home plate to first base ia a feet then by Pythagoras theorem
a2 + a2 = 1202
Solve for a.
Penny
Maelee,
Good grief! If your textbook insists on !!REAL WORLD PROBLEMS!!, why can't the authors get the facts right? The distance between the bases is 90 feet. Consequently, the distance from home to second is a bit over 127 feet.
Chris
Maelee,
To find the distance between the bases you will need to use trig or Pythagoras' theorem: home plate, first base, and second base form a right triangle with two equal legs, so if the distance from home plate to first base is x feet then x2 + x2 = 1202.
To find the area is simpler! Draw a line from home to second, and a line from the midpoint to third. Cut along these lines and put the small triangles (short sides 60 ft) outside the home-first and first-second baselines. You now have a rectangle - what is its area?
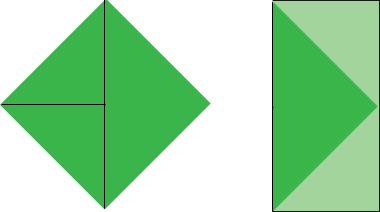
Good Hunting!
RD
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.