An optimization problem

HOME

Math Central

Quandaries & Queries

Question from Marina, a student:

Hello, I have an optimization homework assignment and this question has me stumped..I don't even know where to begin!

A hiker finds herself in a forest 2 km from a long straight road. She wants to walk to her cabin 10 km away and also 2 km from the road. She can walk 8km/hr on the road but only 3km/hr in the forest. She decides to walk thru the forest to the road, along the road, and again thru the forest to her cabin. What angle theta would minimize the total time required for her to reach her cabin?
I'll do my best to copy the diagram here:

                             10km
Hiker_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _Cabin
      \                           |                              /
       \                          |                             /
     f \                      2km                          /
         \                        |                           /
theta   \___________________________ /
                            Road

I know the equation for time is as such: (I am calling the forest distance f and the road r
T = 2f/3 + r/8
But that's as much as I have! please help....

Hi Marina,

I redrew your diagram so that I can label it.

walk

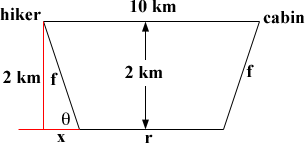
From the diagram r + 2x = 100 km so r = 100 - 2x km. Also sin(θ) = 2/f so f = 2/sin(θ). Write x in terms of a trig function of θ. Using these relationships you can write your expression for the time, T = 2f/3 + r/8 as a function of θ. Now use your knowledge of calculus to find the value of θ that minimizes T.

Write back if you need further assistance,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.