Hi Michelle,

Pythagoras theorem is what you need here.

Suppose that a point (x, y) is on the circle then you can form a right triangle CAB as in the diagram.

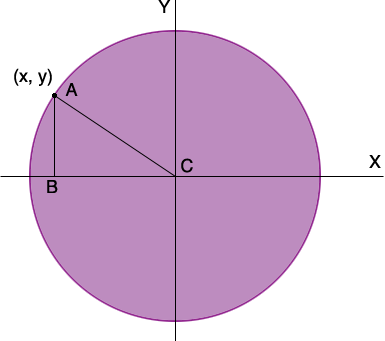
I chose a point in the second quadrant so y is positive but x is negative.

Since the diameter of the circle is 12 its radius is 6 and hence the length |CA| of the line segment form C to A is 6 units. Since y is positive |AB| = y. But x is negative so |BC| = -x. [For example if x = -4 then |BC| = -(-4) = 4.]

Pythagoras theorem for triangle CAB says

|AB|² + |BC|² = |CA|²

or

y² + (-x)² = 6².

Thus

x² + y² = 6².

This is an equation that relates x and y is (x, y) is in the second quadrant. What if (x, y) is in the first quadrant? The third quadrant? The fourth quadrant?

Penny