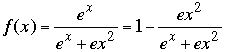| |||
| Math Central | Quandaries & Queries |
|
Question from natalie, a student: I'm trying to graph the function, f(x)= (e^x) / (e^x)+(ex^2) [e to the x divided by e to the x plus e times x squared] I know that there aren't any vertical asymptotes, but is there a horizontal asymptote? and also, I'm stuck on finding the concavity for this graph. I tried to find f "(x), but it came out to be really long and I am not sure how to find the x values for f "(x) without using a graphic calculator. thanks, |
Natalie,
One should use parentheses to make it clear what goes with what. I interpret the denominator to be
ex +ex2.
Begin by dividing the denominator into the numerator (or, more easily, rewrite the top as ex +ex2 - ex2), and you get
You can learn a great deal about the graph of the function without using calculus, by just examining the form of the function.
- f(0) = 1.
- The graph lies in the strip between y = 0 and y = 1.
- For negative x the graph is asymptotic to y = 0.
- For positive x the graph is asymptotic to y = 1.
- For x ≥ 0 the graph goes form f(0) = 1 to some minimum point and then up to the asymptote.
You indicated that your problem is with concavity so I assume you have found the first derivative and determined that the critical points are at x = 0 and x = 2. You can now sketch the graph quite easily.
If you need to find the points where the graph changes concavity then you are faced with solving f"(x) = 0.
Chris and Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.