Question from Neven:

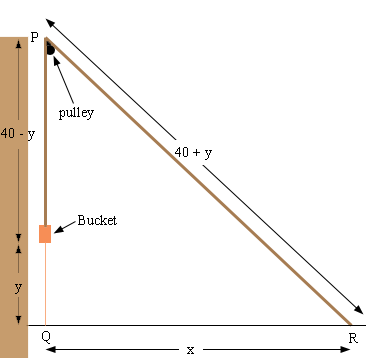
A woman raises a bucket of cement to a platform 40 ft
above her head by means of a rope 80 ft long that passes
over a pulley on the platform. If she holds her end of
the rope firmly at head level and walks away at 5ft/s,
how fast is the bucket rising when she is 30 ft away
from the spot directly below the pulley?
(G. F. Simmons, Calculus with Analytic Geometry, pg.142)
Solution: 3ft/s
I'm having trouble creating a usable diagram of the situation,
and noticing geometric identities need to correctly write the function
y(x) (answering the question - how does the height of bucket- above
the reference point [head of lifter] depend on the change in
horizontal position. Obviously the length of rope does not change,
the rope position creates a right angle... but I cannot seem to be able to
connect all this information together in a single expression at the moment.
As usual, the calculus part is easy... it's setting the problem that's more
difficult. Solve the problem and offer advice to combat such problems in
the future! Thanks in advance!