Hi Rob.

An octagon has eight equal triangular sectors. Therefore, the central angle for each sector is 360 degrees divided by 8, which is 45 degrees.

I presume that 69 inches is the inside diameter (the distance across from side to side) of the hot tub. Therefore the radius is half of that: 34.5 inches. This means each triangular sector is an isosceles triangle with common sides of 34.5 inches each joined by an angle of 45 degrees. The question is therefore, what is the length of the third side?

There is an easy formula for calculating the length of the unique leg of an isosceles triangle when you know the length of the common sides and the (pivot) angle between them. I'll show you how to come up with that:

Any isosceles triangle can be divided into two congruent right triangles just by connecting the pivot to the midpoint of the unique side. Therefore, each of these right triangles has an angle of 1/2 the original angle (it is bisected) and across from this is half the unique side length of the isosceles triangle. The hypotenuse of the right triangle is the same as the common leg of the isosceles triangle.

Using sine, the relationship is easy: Sin = opposite/hypotenuse. Thus,

Sin (A/2) = (x/2) / r

where A is the pivot angle (45 degrees), x is the length of the unique side of the isosceles triangle, and r is the length of the common side (34.5 inches). When we solve for x and then substitute in these known values, we get:
x = 2r Sin (A/2)

x = 2(34.5) Sin (45/2) = 69 sin (22.5) = 69 (0.3827) = 26.41 inches.

Thus your bench pieces need to have a length not exceeding 26.41 inches (about 26 3/8" should be right), if everything is precise.

The "cuts" need to be 22.5 degree cuts. If you are using a long piece of material, you should be able to waste very little material by cutting like this:

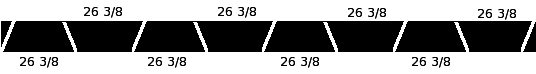
If you can, send us a photo if you build it!

Cheers,
Stephen La Rocque.