| |||
| Math Central | Quandaries & Queries |
|
I am in the process of making an Excel spreadsheet in which our sales team just needs to enter the outside diameter, inside diameter, and number of segments to price ring gaskets that are too big to fit on a sheet of material and need to be cut into segments. With your help I was able to create a spread sheet that can calculate the Chord lengths, and Segment height on a single gasket segment. I am now stuck trying to come up with a formula to figure out the height of the second segment when it is stacked on the first segment, then use it to add more depending on the quantity of segments needed. I have an illustration below showing 2 segments (of a gasket that was segmented into 4 pieces) stacked together. I need to find a formula to get the dimension from “A” to “B”. |
Robert,
I labeled three points in the diagram you sent.
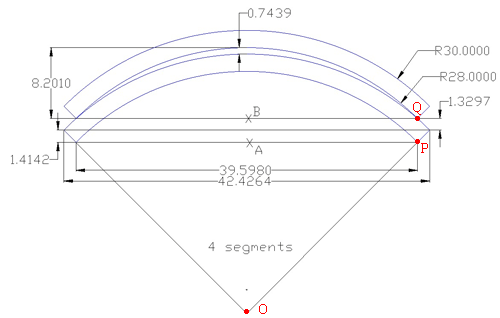
Put a coordinate system on your diagram with the origin at O then the inside edge of the first gasket segment is part of the circle x2 + y2 = 282 and the outside edge is part of the circle x2 + y2 = 302. The x-coordinate of P is 39.5980/2 and hence the y-coordinate of P is given by y2 = 282 - (39.5980/2)2. Likewise Q has x-coordinate 39.5980/2 and hence the y-coordinate of Q is given by y2 = 302 - (39.5980/2)2. The distance you need, the distance between A and B is the distance between P and Q which is
√[302 - (39.5980/2)2] - √[282 - (39.5980/2)2]
which I get to be 2.7399 (inches I presume). Your diagram gives this as 1.4142 + 1.3297 = 2.7439 so we agree to 3 decimal places.
I hope this helps. Write back if you need anything further,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.