Rocco,

I'm going o look at a somewhat similar but simpler problem.

Which values of x satisfy x³ - 8x² + 16x > 0?

I see this in a graphical way. I imagine that I am walking along the curve f(x) = x³ - 8x² + 16x and ask when I am above the line y = 0. The key is to ask when might I cross from one side of y = 0 to the other. If I cross from one side of y = 0 to the other I must go through a point where y = 0, that is a point where

x³ - 8x² + 16x = 0.

To find such points I factor x³ - 8x² + 16x and obtain

x(x - 4)² = 0.

This has solutions x = 0 and x = 4 and these are the only possible x-values where I might cross x = 0.

Now suppose I am at a point on the graph with x-coordinate less than 0, say for example x = -10. Then f(-10) = -10(-10 - 4)² = -1960 so I am below y = 0. The first place I can cross y = 0 at x = 0 so where am I when x = 1? f(1) = 1(1-4)² = 9 so I am above y = 0. The next place I can cross y = 0 is at x = 4 so where am I if x > 4, say x = 5? f(5) = 5(5-4)² = 5 so I am still above y = 0 and I can't cross y = 0 again. Thus the answer to

Which values of x satisfy x³ - 8x² + 16x > 0?

is for 0 < x < 4 and for x > 4.

Here is the graph

.

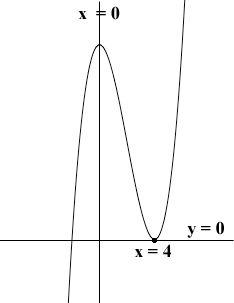For your problem

Which values of x satisfy (x - 2)/(x + 4) <7?

first solve (x - 2)/(x + 4) = 7 to see where the graph of f(x) = (x - 2)/(x + 4) crosses the line y = 7. You should find one x-value. The complication in your problem is what happens at x = -4. At this point the denominator of f(x) = (x - 2)/(x + 4) is zero and there is no point on the curve. The graph near x = -4 might look something like

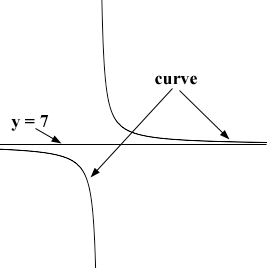
and the curve might then move from one side of y = 7 to the other without actually crossing y = 7. Thus, as in my problem you have two x-values where the graph might move from one side of y = 7 to the other, the x-value you found by solving (x - 2)/(x + 4) = 7 and x = -4.

Continue as I did for the simpler problem. Write back if you need further assistance.

Harley