| |||
| Math Central | Quandaries & Queries |
|
Question from Ron, a student: Hello I'm trying to find out the intervals where the function is positive and negative. I have tried the right and left side of each x-intercepts, but I still don't understand the thank you for your help |
Hi Ron,
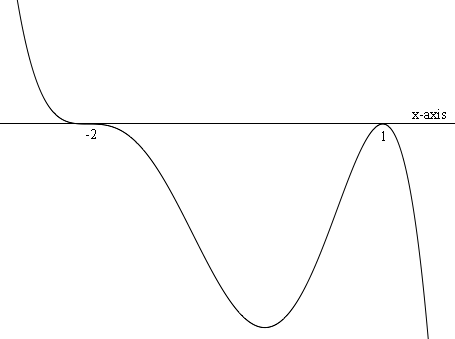
I want to illustrate with the function f(x) = -(1/4) (x - 1)2 (x + 2)3.
The x-intercepts are 1 and -2 and these two intercepts divide the line into three intervals.
![]()
To the left of -2 I chose x = -3. f(-3) = -(1/4) (-3 - 1)2 (-3 + 2)3 which is positive so the function is positive on the interval -∞ < x < -2.
Between -2 and 1 I chose x = 0. f(0) = -(1/4) (0 - 1)2 (0 + 2)3 which is negative so the function is negative on the interval -2 < x < 1.
To the right of 1 I chose x = 2. f(2) = -(1/4) (2 - 1)2 (2 + 2)3 which is negative so the function is negative on the interval 1 < x < ∞.
Here is a sketch of the function.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.