Draw a diagram!

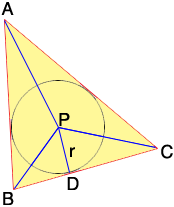
P is the centre of the inscribed circle and r is its radius. Join P to each of the triangle vertices to partition the triangle ABC into three triangles. Look at one of these triangles PBC. D is the point on BC where the inscribed triangle touches the side. BC is tangent to the circle at this point so angle PDC is a right angle and hence r is the height of triangle PBC. What is the area of triangle PBC? In a similar way find the areas of triangles PCA and PAB. Their sum is the area of triangle ABC.

Penny