| |||
| Math Central | Quandaries & Queries |
|
hi, would u please help me in this question, A man starts walking north at 4 ft/s from a point P. 5 minutes later a woman starts walking south at 5 ft/s from a point 500 ft due east of P. At what rate are the people moving apart 15 minute after the woman starts walking? |
Five minutes after the man starts walking is 5 × 60 = 300 seconds so he has gone 4 × 300 = 1200 feet north. He continues to walk north at a rate of 4 feet north every second and the woman walks 5 feet south every second. Hence t seconds after the woman starts to walk their positions are as in the diagram.
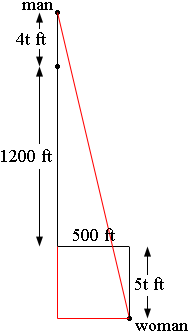
The long red line indicates the distance between the man and woman. You want to know the rate at which this distance is changing when t = 15 × 60 seconds. I added the other two red line segments to complete a right triangle. Use Pythagoras theorem to write an expression for the distance between the man and woman at time t. Use calculus to determine the rate at which this distance is changing.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.